Appendix A — AP Exam Formula Sheet
Here is the original AP Statistics Formula Sheet developed by Collegeboard.
A.1 Descriptive Statistics
\[ \begin{aligned} \bar x &= \frac{1}{n}\sum x_i = \frac{\sum x_i}{n} \\\\ s_x &= \sqrt{\frac{1}{n-1}\sum (x_i - \bar x)^2} = \sqrt{\frac{\sum(x_i -\bar x)^2}{n - 1}}\\\\ \hat y &= a + bx \\\\ \bar y &= a + b \bar x\\\\ r &= \frac{1}{n-1}\sum \left( \frac{x_i - \bar x}{s_x}\right) \left( \frac{y_i -\bar y}{s_y}\right)\\\\ b &= r \frac{s_y}{s_x} \end{aligned} \]
A.2 Probability and Distributions
\[ \begin{aligned} P(A \cup B) &= P(A) + P(B) - P(A \cap B) \\\\ P(A | B) &= \frac{P(A \cap B)}{P(B)} \end{aligned} \]
| Probability Distribution | Mean | Standard Deviation |
|---|---|---|
| Discrete random variable, \(X\) | \(\mu_X = E(X) = \sum x_i P(x_i)\) | \(\sigma_X = \sqrt{\sum \left( x_i - \mu_X \right) ^2 P \left( x_i \right)}\) |
| If \(X\) has a binomial distribution with parameters \(n\) and \(p\), then: \[P(X = x) = {n \choose x} p^x (1 - p)^{n - x}\] where \(x = 0, 1, 2, 3, ..., n\) |
\(\mu_X = np\) | \(\sigma_X = \sqrt{np(1-p)}\) |
| If \(X\) has a geometric distribution with parameter \(p\), then: \[P(X = x) = (1 - p)^{x - 1} p\] where \(x = 1, 2, 3, ...\) |
\(\mu_X = \frac{1}{p}\) | \(\sigma_X = \frac{\sqrt{1-p}}{p}\) |
A.3 Sampling Distributions and Inferential Statistics
\[\text{Standardized test statistic:}~~~~ \frac{\text{statistic} - \text{parameter}} {\text{standard error of the statistic}}\]
\[\text{Confidence interval:}~~~~ \text{statistic} \pm (\text{critical value}) (\text{standard error of statistic})\]
\[\text{Chi-square statistic:}~~~~ \chi^2 = \sum \frac{(\text{observed} - \text{expected})^2}{\text{expected}}\]
A.3.1 Sampling distributions for proportions:
| Random Variable | Parameters of Sampling Distribution (mean) | Parameters of Sampling Distribution (standard deviation) | Standard Error* of Sample Statistic |
|---|---|---|---|
| For one population: \(\hat p\) |
\(\mu_{\hat p} = p\) | \(\sigma_{\hat p} = \sqrt{\frac{p(1-p)}{n}}\) | \(s_{\hat p} = \sqrt{\frac{\hat p (1 - \hat p)}{n}}\) |
| For two populations: \(\hat p_1 - \hat p_2\) |
\(\mu_{\hat p_1 - \hat p_2} = p_1 - p_2\) | \(\sigma_{\hat p_1 - \hat p_2}= \sqrt{\frac{p_1(1-p_1)}{n_1} + \frac{p_2(1-p_2)}{n_2}}\) | \(s_{\hat p_1 - \hat p_2}= \sqrt{\frac{\hat p_1(1- \hat p_1)}{n_1} + \frac{\hat p_2(1- \hat p_2)}{n_2}}\) When \(p_1 = p_2\) is assumed: \(s_{\hat p_1 -\hat p_2} = \sqrt{\hat p_c (1 - \hat p_c) \left( \frac{1}{n_1} + \frac{1}{n_2} \right)}\) where \(\hat p_c = \frac{X_1 + X_2}{n_1 + n_2}\) |
A.3.2 Sampling distributions for means:
| Random Variable | Parameters of Sampling Distribution (mean) | Parameters of Sampling Distribution (standard deviation) | Standard Error* of Sample Statistic |
|---|---|---|---|
| For one population: \(\overline{X}\) |
\(\mu_{\overline X} = \mu\) | \(\sigma_{\overline X} = \frac{\sigma}{\sqrt n}\) | \(s_{\overline X} = \frac{s}{\sqrt n}\) |
| For two populations: \(\overline{X_1} - \overline{X_2}\) |
\(\mu_{\overline{X_1} - \overline{X_2}} = \mu_1 - \mu_2\) | \(\sigma_{\overline{X_1} - \overline{X_2}} = \sqrt{\frac{\sigma_1^2}{n_1} + \frac{\sigma_2^2}{n_2}}\) | \(s_{\overline{X_1} - \overline{X_2}} = \sqrt{\frac{s_1^2}{n_1} + \frac{s_2^2}{n_2}}\) |
A.3.3 Sampling distributions for simple linear regression:
| Random Variable | Parameters of Sampling Distribution (mean) | Parameters of Sampling Distribution (standard deviation) | Standard Error* of Sample Statistic |
|---|---|---|---|
| For slope: \(b\) |
\(\mu_b = \beta\) | \(\sigma_{b} = \frac{\sigma}{\sigma_x \sqrt n}\), where \(\sigma_x = \sqrt{\frac{\sum (x_i - \bar x)^2}{n}}\) |
\(s_{b} = \frac{s}{s_x \sqrt{n-1}}\) , where \(s = \sqrt{\frac{\sum (y_i - \hat y_i)^2)}{n - 2}}\) and \(s_x = \sqrt{\frac{\sum (x_i - \bar x)^2}{n - 1}}\) |
*Standard deviation is a measurement of variability from the theoretical population. Standard error is the estimate of the standard deviation. If the standard deviation of the statistic is assumed to be known, then the standard deviation should be used instead of the standard error.
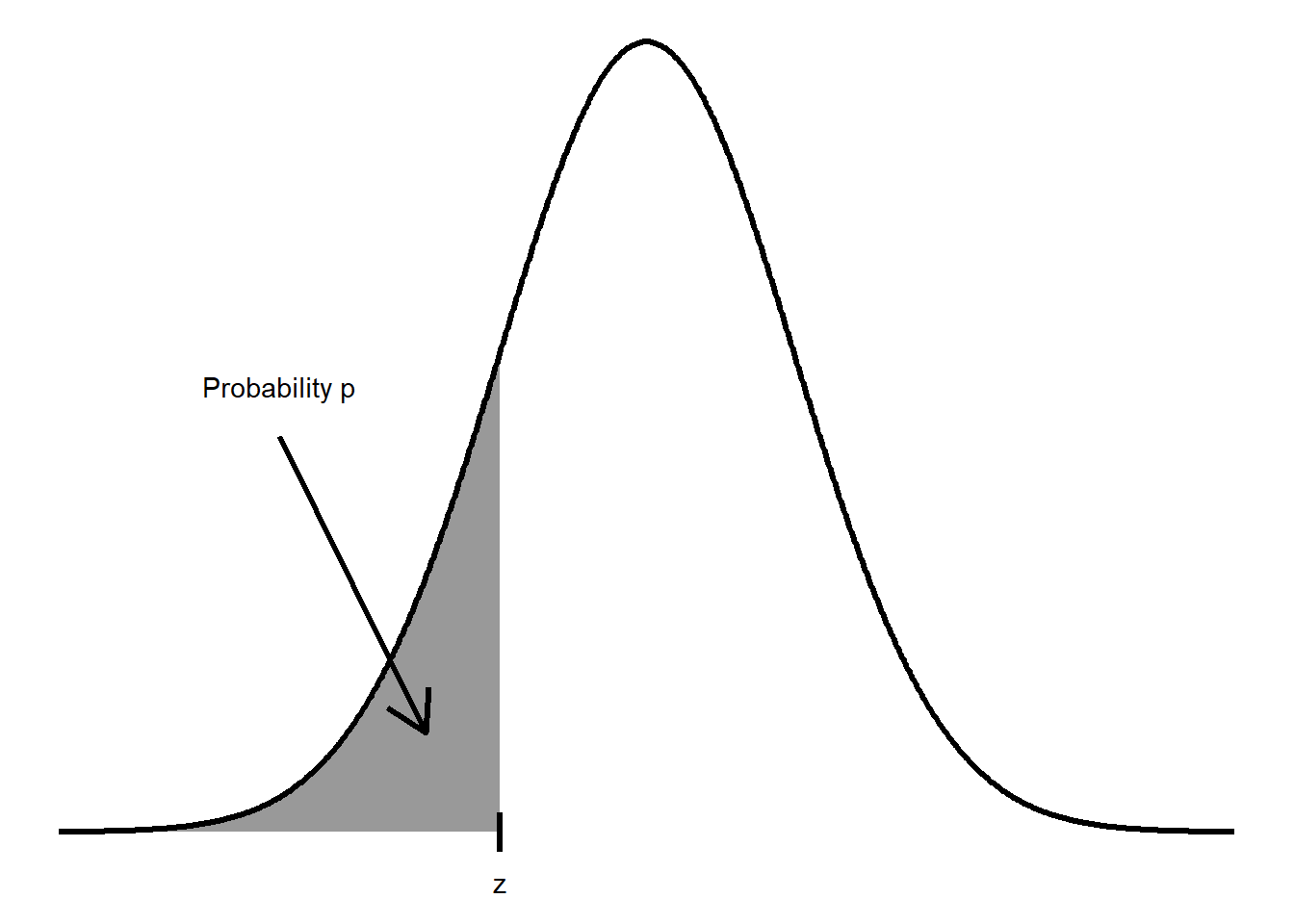
A.4 Table A: Standard normal probabilities
Click for table of standard normal probabilities
Table entry for \(z\) is the probability lying below \(z\).
| \(z\) | 0.00 | 0.01 | 0.02 | 0.03 | 0.04 | 0.05 | 0.06 | 0.07 | 0.08 | 0.09 |
|---|---|---|---|---|---|---|---|---|---|---|
| -3.4 | 0.0003 | 0.0003 | 0.0003 | 0.0003 | 0.0003 | 0.0003 | 0.0003 | 0.0003 | 0.0003 | 0.0002 |
| -3.3 | 0.0005 | 0.0005 | 0.0005 | 0.0004 | 0.0004 | 0.0004 | 0.0004 | 0.0004 | 0.0004 | 0.0003 |
| -3.2 | 0.0007 | 0.0007 | 0.0006 | 0.0006 | 0.0006 | 0.0006 | 0.0006 | 0.0005 | 0.0005 | 0.0005 |
| -3.1 | 0.0010 | 0.0009 | 0.0009 | 0.0009 | 0.0008 | 0.0008 | 0.0008 | 0.0008 | 0.0007 | 0.0007 |
| -3.0 | 0.0013 | 0.0013 | 0.0013 | 0.0012 | 0.0012 | 0.0011 | 0.0011 | 0.0011 | 0.0010 | 0.0010 |
| -2.9 | 0.0019 | 0.0018 | 0.0018 | 0.0017 | 0.0016 | 0.0016 | 0.0015 | 0.0015 | 0.0014 | 0.0014 |
| -2.8 | 0.0026 | 0.0025 | 0.0024 | 0.0023 | 0.0023 | 0.0022 | 0.0021 | 0.0021 | 0.0020 | 0.0019 |
| -2.7 | 0.0035 | 0.0034 | 0.0033 | 0.0032 | 0.0031 | 0.0030 | 0.0029 | 0.0028 | 0.0027 | 0.0026 |
| -2.6 | 0.0047 | 0.0045 | 0.0044 | 0.0043 | 0.0041 | 0.0040 | 0.0039 | 0.0038 | 0.0037 | 0.0036 |
| -2.5 | 0.0062 | 0.0060 | 0.0059 | 0.0057 | 0.0055 | 0.0054 | 0.0052 | 0.0051 | 0.0049 | 0.0048 |
| -2.4 | 0.0082 | 0.0080 | 0.0078 | 0.0075 | 0.0073 | 0.0071 | 0.0069 | 0.0068 | 0.0066 | 0.0064 |
| -2.3 | 0.0107 | 0.0104 | 0.0102 | 0.0099 | 0.0096 | 0.0094 | 0.0091 | 0.0089 | 0.0087 | 0.0084 |
| -2.2 | 0.0139 | 0.0136 | 0.0132 | 0.0129 | 0.0125 | 0.0122 | 0.0119 | 0.0116 | 0.0113 | 0.0110 |
| -2.1 | 0.0179 | 0.0174 | 0.017 | 0.0166 | 0.0162 | 0.0158 | 0.0154 | 0.0150 | 0.0146 | 0.0143 |
| -2.0 | 0.0228 | 0.0222 | 0.0217 | 0.0212 | 0.0207 | 0.0202 | 0.0197 | 0.0192 | 0.0188 | 0.0183 |
| -1.9 | 0.0287 | 0.0281 | 0.0274 | 0.0268 | 0.0262 | 0.0256 | 0.0250 | 0.0244 | 0.0239 | 0.0233 |
| -1.8 | 0.0359 | 0.0351 | 0.0344 | 0.0336 | 0.0329 | 0.0322 | 0.0314 | 0.0307 | 0.0301 | 0.0294 |
| -1.7 | 0.0446 | 0.0436 | 0.0427 | 0.0418 | 0.0409 | 0.0401 | 0.0392 | 0.0384 | 0.0375 | 0.0367 |
| -1.6 | 0.0548 | 0.0537 | 0.0526 | 0.0516 | 0.0505 | 0.0495 | 0.0485 | 0.0475 | 0.0465 | 0.0455 |
| -1.5 | 0.0668 | 0.0655 | 0.0643 | 0.0630 | 0.0618 | 0.0606 | 0.0594 | 0.0582 | 0.0571 | 0.0559 |
| -1.4 | 0.0808 | 0.0793 | 0.0778 | 0.0764 | 0.0749 | 0.0735 | 0.0721 | 0.0708 | 0.0694 | 0.0681 |
| -1.3 | 0.0968 | 0.0951 | 0.0934 | 0.0918 | 0.0901 | 0.0885 | 0.0869 | 0.0853 | 0.0838 | 0.0823 |
| -1.2 | 0.1151 | 0.1131 | 0.1112 | 0.1093 | 0.1075 | 0.1056 | 0.1038 | 0.1020 | 0.1003 | 0.0985 |
| -1.1 | 0.1357 | 0.1335 | 0.1314 | 0.1292 | 0.1271 | 0.1251 | 0.1230 | 0.1210 | 0.1190 | 0.1170 |
| -1.0 | 0.1587 | 0.1562 | 0.1539 | 0.1515 | 0.1492 | 0.1469 | 0.1446 | 0.1423 | 0.1401 | 0.1379 |
| -0.9 | 0.1841 | 0.1814 | 0.1788 | 0.1762 | 0.1736 | 0.1711 | 0.1685 | 0.1660 | 0.1635 | 0.1611 |
| -0.8 | 0.2119 | 0.2090 | 0.2061 | 0.2033 | 0.2005 | 0.1977 | 0.1949 | 0.1922 | 0.1894 | 0.1867 |
| -0.7 | 0.2420 | 0.2389 | 0.2358 | 0.2327 | 0.2296 | 0.2266 | 0.2236 | 0.2206 | 0.2177 | 0.2148 |
| -0.6 | 0.2743 | 0.2709 | 0.2676 | 0.2643 | 0.2611 | 0.2578 | 0.2546 | 0.2514 | 0.2483 | 0.2451 |
| -0.5 | 0.3085 | 0.305 | 0.3015 | 0.2981 | 0.2946 | 0.2912 | 0.2877 | 0.2843 | 0.281 | 0.2776 |
| -0.4 | 0.3446 | 0.3409 | 0.3372 | 0.3336 | 0.3300 | 0.3264 | 0.3228 | 0.3192 | 0.3156 | 0.3121 |
| -0.3 | 0.3821 | 0.3783 | 0.3745 | 0.3707 | 0.3669 | 0.3632 | 0.3594 | 0.3557 | 0.3520 | 0.3483 |
| -0.2 | 0.4207 | 0.4168 | 0.4129 | 0.4090 | 0.4052 | 0.4013 | 0.3974 | 0.3936 | 0.3897 | 0.3859 |
| -0.1 | 0.4602 | 0.4562 | 0.4522 | 0.4483 | 0.4443 | 0.4404 | 0.4364 | 0.4325 | 0.4286 | 0.4247 |
| 0.0 | 0.5000 | 0.4960 | 0.4920 | 0.4880 | 0.4840 | 0.4801 | 0.4761 | 0.4721 | 0.4681 | 0.4641 |
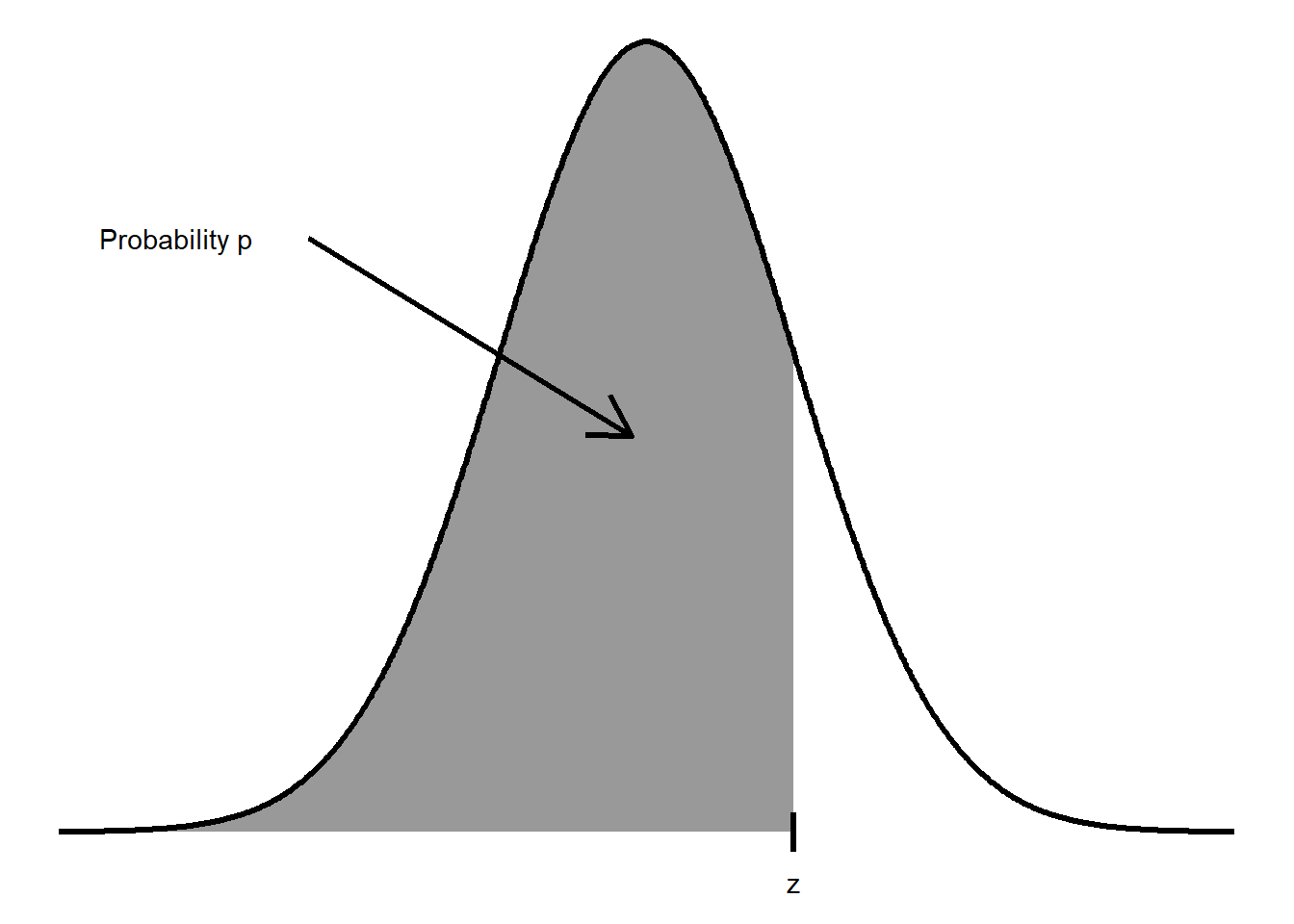
Click for table of standard normal probabilities (continued)
Table entry for \(z\) is the probability lying below \(z\).
| \(z\) | 0.00 | 0.01 | 0.02 | 0.03 | 0.04 | 0.05 | 0.06 | 0.07 | 0.08 | 0.09 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0.0 | 0.5000 | 0.5040 | 0.5080 | 0.5120 | 0.5160 | 0.5199 | 0.5239 | 0.5279 | 0.5319 | 0.5359 |
| 0.1 | 0.5398 | 0.5438 | 0.5478 | 0.5517 | 0.5557 | 0.5596 | 0.5636 | 0.5675 | 0.5714 | 0.5753 |
| 0.2 | 0.5793 | 0.5832 | 0.5871 | 0.5910 | 0.5948 | 0.5987 | 0.6026 | 0.6064 | 0.6103 | 0.6141 |
| 0.3 | 0.6179 | 0.6217 | 0.6255 | 0.6293 | 0.6331 | 0.6368 | 0.6406 | 0.6443 | 0.6480 | 0.6517 |
| 0.4 | 0.6554 | 0.6591 | 0.6628 | 0.6664 | 0.6700 | 0.6736 | 0.6772 | 0.6808 | 0.6844 | 0.6879 |
| 0.5 | 0.6915 | 0.6950 | 0.6985 | 0.7019 | 0.7054 | 0.7088 | 0.7123 | 0.7157 | 0.7190 | 0.7224 |
| 0.6 | 0.7257 | 0.7291 | 0.7324 | 0.7357 | 0.7389 | 0.7422 | 0.7454 | 0.7486 | 0.7517 | 0.7549 |
| 0.7 | 0.7580 | 0.7611 | 0.7642 | 0.7673 | 0.7704 | 0.7734 | 0.7764 | 0.7794 | 0.7823 | 0.7852 |
| 0.8 | 0.7881 | 0.7910 | 0.7939 | 0.7967 | 0.7995 | 0.8023 | 0.8051 | 0.8078 | 0.8106 | 0.8133 |
| 0.9 | 0.8159 | 0.8186 | 0.8212 | 0.8238 | 0.8264 | 0.8289 | 0.8315 | 0.8340 | 0.8365 | 0.8389 |
| 1.0 | 0.8413 | 0.8438 | 0.8461 | 0.8485 | 0.8508 | 0.8531 | 0.8554 | 0.8577 | 0.8599 | 0.8621 |
| 1.1 | 0.8643 | 0.8665 | 0.8686 | 0.8708 | 0.8729 | 0.8749 | 0.8770 | 0.8790 | 0.8810 | 0.8830 |
| 1.2 | 0.8849 | 0.8869 | 0.8888 | 0.8907 | 0.8925 | 0.8944 | 0.8962 | 0.8980 | 0.8997 | 0.9015 |
| 1.3 | 0.9032 | 0.9049 | 0.9066 | 0.9082 | 0.9099 | 0.9115 | 0.9131 | 0.9147 | 0.9162 | 0.9177 |
| 1.4 | 0.9192 | 0.9207 | 0.9222 | 0.9236 | 0.9251 | 0.9265 | 0.9279 | 0.9292 | 0.9306 | 0.9319 |
| 1.5 | 0.9332 | 0.9345 | 0.9357 | 0.9370 | 0.9382 | 0.9394 | 0.9406 | 0.9418 | 0.9429 | 0.9441 |
| 1.6 | 0.9452 | 0.9463 | 0.9474 | 0.9484 | 0.9495 | 0.9505 | 0.9515 | 0.9525 | 0.9535 | 0.9545 |
| 1.7 | 0.9554 | 0.9564 | 0.9573 | 0.9582 | 0.9591 | 0.9599 | 0.9608 | 0.9616 | 0.9625 | 0.9633 |
| 1.8 | 0.9641 | 0.9649 | 0.9656 | 0.9664 | 0.9671 | 0.9678 | 0.9686 | 0.9693 | 0.9699 | 0.9706 |
| 1.9 | 0.9713 | 0.9719 | 0.9726 | 0.9732 | 0.9738 | 0.9744 | 0.9750 | 0.9756 | 0.9761 | 0.9767 |
| 2.0 | 0.9772 | 0.9778 | 0.9783 | 0.9788 | 0.9793 | 0.9798 | 0.9803 | 0.9808 | 0.9812 | 0.9817 |
| 2.1 | 0.9821 | 0.9826 | 0.9830 | 0.9834 | 0.9838 | 0.9842 | 0.9846 | 0.9850 | 0.9854 | 0.9857 |
| 2.2 | 0.9861 | 0.9864 | 0.9868 | 0.9871 | 0.9875 | 0.9878 | 0.9881 | 0.9884 | 0.9887 | 0.9890 |
| 2.3 | 0.9893 | 0.9896 | 0.9898 | 0.9901 | 0.9904 | 0.9906 | 0.9909 | 0.9911 | 0.9913 | 0.9916 |
| 2.4 | 0.9918 | 0.9920 | 0.9922 | 0.9925 | 0.9927 | 0.9929 | 0.9931 | 0.9932 | 0.9934 | 0.9936 |
| 2.5 | 0.9938 | 0.9940 | 0.9941 | 0.9943 | 0.9945 | 0.9946 | 0.9948 | 0.9949 | 0.9951 | 0.9952 |
| 2.6 | 0.9953 | 0.9955 | 0.9956 | 0.9957 | 0.9959 | 0.9960 | 0.9961 | 0.9962 | 0.9963 | 0.9964 |
| 2.7 | 0.9965 | 0.9966 | 0.9967 | 0.9968 | 0.9969 | 0.9970 | 0.9971 | 0.9972 | 0.9973 | 0.9974 |
| 2.8 | 0.9974 | 0.9975 | 0.9976 | 0.9977 | 0.9977 | 0.9978 | 0.9979 | 0.9979 | 0.9980 | 0.9981 |
| 2.9 | 0.9981 | 0.9982 | 0.9982 | 0.9983 | 0.9984 | 0.9984 | 0.9985 | 0.9985 | 0.9986 | 0.9986 |
| 3.0 | 0.9987 | 0.9987 | 0.9987 | 0.9988 | 0.9988 | 0.9989 | 0.9989 | 0.9989 | 0.9990 | 0.9990 |
| 3.1 | 0.9990 | 0.9991 | 0.9991 | 0.9991 | 0.9992 | 0.9992 | 0.9992 | 0.9992 | 0.9993 | 0.9993 |
| 3.2 | 0.9993 | 0.9993 | 0.9994 | 0.9994 | 0.9994 | 0.9994 | 0.9994 | 0.9995 | 0.9995 | 0.9995 |
| 3.3 | 0.9995 | 0.9995 | 0.9995 | 0.9996 | 0.9996 | 0.9996 | 0.9996 | 0.9996 | 0.9996 | 0.9997 |
| 3.4 | 0.9997 | 0.9997 | 0.9997 | 0.9997 | 0.9997 | 0.9997 | 0.9997 | 0.9997 | 0.9997 | 0.9998 |
A.5 Table B: \(t\) distribution critical values
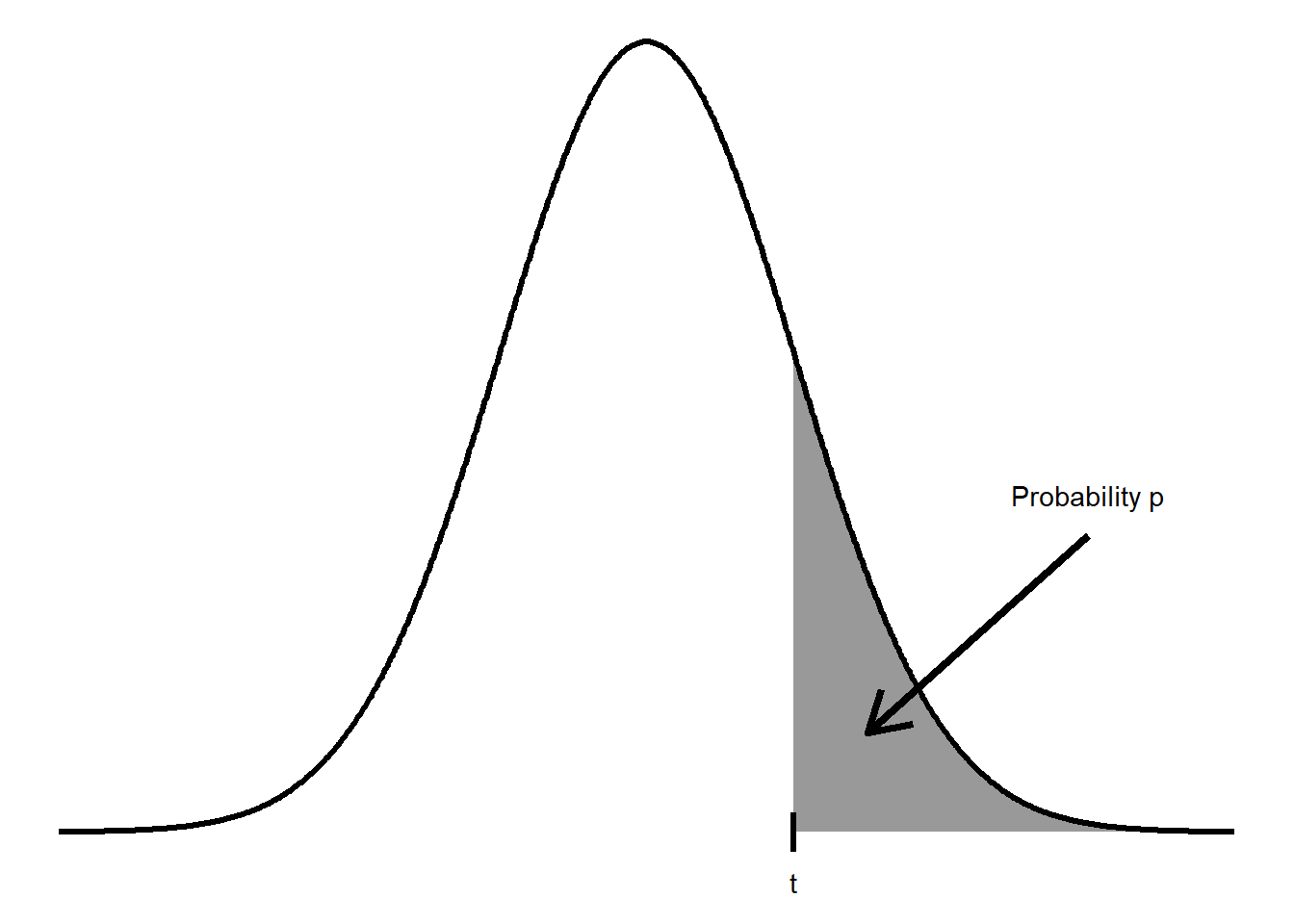
Click here for table of \(t\) distribution critical values
Table entry for \(p\) and \(C\) is the point \(t*\) with probability \(p\) lying above it and probability \(C\) lying between \(-t*\) and \(t*\).
| df | Tail Probability \(p\) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.25 | 0.20 | 0.15 | 0.10 | 0.05 | 0.025 | 0.02 | 0.01 | 0.005 | 0.0025 | 0.001 | 0.0005 | |
| 1 | 1.000 | 1.376 | 1.963 | 3.078 | 6.314 | 12.71 | 15.89 | 31.82 | 63.66 | 127.3 | 318.3 | 636.6 |
| 2 | 0.816 | 1.061 | 1.386 | 1.886 | 2.920 | 4.303 | 4.849 | 6.965 | 9.925 | 14.09 | 22.33 | 31.60 |
| 3 | 0.765 | 0.978 | 1.250 | 1.638 | 2.353 | 3.182 | 3.482 | 4.541 | 5.841 | 7.453 | 10.21 | 12.92 |
| 4 | 0.741 | 0.941 | 1.190 | 1.533 | 2.132 | 2.776 | 2.999 | 3.747 | 4.604 | 5.598 | 7.173 | 8.610 |
| 5 | 0.727 | 0.920 | 1.156 | 1.476 | 2.015 | 2.571 | 2.757 | 3.365 | 4.032 | 4.773 | 5.893 | 6.869 |
| 6 | 0.718 | 0.906 | 1.134 | 1.440 | 1.943 | 2.447 | 2.612 | 3.143 | 3.707 | 4.317 | 5.208 | 5.959 |
| 7 | 0.711 | 0.896 | 1.119 | 1.415 | 1.895 | 2.365 | 2.517 | 2.998 | 3.499 | 4.029 | 4.785 | 5.408 |
| 8 | 0.706 | 0.889 | 1.108 | 1.397 | 1.860 | 2.306 | 2.449 | 2.896 | 3.355 | 3.833 | 4.501 | 5.041 |
| 9 | 0.703 | 0.883 | 1.100 | 1.383 | 1.833 | 2.262 | 2.398 | 2.821 | 3.250 | 3.690 | 4.297 | 4.781 |
| 10 | 0.700 | 0.879 | 1.093 | 1.372 | 1.812 | 2.228 | 2.359 | 2.764 | 3.169 | 3.581 | 4.144 | 4.587 |
| 11 | 0.697 | 0.876 | 1.088 | 1.363 | 1.796 | 2.201 | 2.328 | 2.718 | 3.106 | 3.497 | 4.025 | 4.437 |
| 12 | 0.695 | 0.873 | 1.083 | 1.356 | 1.782 | 2.179 | 2.303 | 2.681 | 3.055 | 3.428 | 3.930 | 4.318 |
| 13 | 0.694 | 0.870 | 1.079 | 1.350 | 1.771 | 2.160 | 2.282 | 2.650 | 3.012 | 3.372 | 3.852 | 4.221 |
| 14 | 0.692 | 0.868 | 1.076 | 1.345 | 1.761 | 2.145 | 2.264 | 2.624 | 2.977 | 3.326 | 3.787 | 4.140 |
| 15 | 0.691 | 0.866 | 1.074 | 1.341 | 1.753 | 2.131 | 2.249 | 2.602 | 2.947 | 3.286 | 3.733 | 4.073 |
| 16 | 0.690 | 0.865 | 1.071 | 1.337 | 1.746 | 2.120 | 2.235 | 2.583 | 2.921 | 3.252 | 3.686 | 4.015 |
| 17 | 0.689 | 0.863 | 1.069 | 1.333 | 1.740 | 2.110 | 2.224 | 2.567 | 2.898 | 3.222 | 3.646 | 3.965 |
| 18 | 0.688 | 0.862 | 1.067 | 1.330 | 1.734 | 2.101 | 2.214 | 2.552 | 2.878 | 3.197 | 3.610 | 3.922 |
| 19 | 0.688 | 0.861 | 1.066 | 1.328 | 1.729 | 2.093 | 2.205 | 2.539 | 2.861 | 3.174 | 3.579 | 3.883 |
| 20 | 0.687 | 0.860 | 1.064 | 1.325 | 1.725 | 2.086 | 2.197 | 2.528 | 2.845 | 3.153 | 3.552 | 3.850 |
| 21 | 0.686 | 0.859 | 1.063 | 1.323 | 1.721 | 2.080 | 2.189 | 2.518 | 2.831 | 3.135 | 3.527 | 3.819 |
| 22 | 0.686 | 0.858 | 1.061 | 1.321 | 1.717 | 2.074 | 2.183 | 2.508 | 2.819 | 3.119 | 3.505 | 3.792 |
| 23 | 0.685 | 0.858 | 1.060 | 1.319 | 1.714 | 2.069 | 2.177 | 2.500 | 2.807 | 3.104 | 3.485 | 3.768 |
| 24 | 0.685 | 0.857 | 1.059 | 1.318 | 1.711 | 2.064 | 2.172 | 2.492 | 2.797 | 3.091 | 3.467 | 3.745 |
| 25 | 0.684 | 0.856 | 1.058 | 1.316 | 1.708 | 2.060 | 2.167 | 2.485 | 2.787 | 3.078 | 3.450 | 3.725 |
| 26 | 0.684 | 0.856 | 1.058 | 1.315 | 1.706 | 2.056 | 2.162 | 2.479 | 2.779 | 3.067 | 3.435 | 3.707 |
| 27 | 0.684 | 0.855 | 1.057 | 1.314 | 1.703 | 2.052 | 2.158 | 2.473 | 2.771 | 3.057 | 3.421 | 3.690 |
| 28 | 0.683 | 0.855 | 1.056 | 1.313 | 1.701 | 2.048 | 2.154 | 2.467 | 2.763 | 3.047 | 3.408 | 3.674 |
| 29 | 0.683 | 0.854 | 1.055 | 1.311 | 1.699 | 2.045 | 2.150 | 2.462 | 2.756 | 3.038 | 3.396 | 3.659 |
| 30 | 0.683 | 0.854 | 1.055 | 1.310 | 1.697 | 2.042 | 2.147 | 2.457 | 2.750 | 3.030 | 3.385 | 3.646 |
| 40 | 0.681 | 0.851 | 1.050 | 1.303 | 1.684 | 2.021 | 2.123 | 2.423 | 2.704 | 2.971 | 3.307 | 3.551 |
| 50 | 0.679 | 0.849 | 1.047 | 1.299 | 1.676 | 2.009 | 2.109 | 2.403 | 2.678 | 2.937 | 3.261 | 3.496 |
| 60 | 0.679 | 0.848 | 1.045 | 1.296 | 1.671 | 2.000 | 2.099 | 2.390 | 2.660 | 2.915 | 3.232 | 3.460 |
| 80 | 0.678 | 0.846 | 1.043 | 1.292 | 1.664 | 1.990 | 2.088 | 2.374 | 2.639 | 2.887 | 3.195 | 3.416 |
| 100 | 0.677 | 0.845 | 1.042 | 1.290 | 1.660 | 1.984 | 2.081 | 2.364 | 2.626 | 2.871 | 3.174 | 3.390 |
| 1000 | 0.675 | 0.842 | 1.037 | 1.282 | 1.646 | 1.962 | 2.056 | 2.330 | 2.581 | 2.813 | 3.098 | 3.300 |
| \(\infty\) | 0.674 | 0.842 | 1.036 | 1.282 | 1.645 | 1.960 | 2.054 | 2.326 | 2.576 | 2.807 | 3.090 | 3.291 |
| 50% | 60% | 70% | 80% | 90% | 95% | 96% | 98% | 99% | 99.50% | 99.8 | 99.99% | |
| Confidence Level \(C\) | ||||||||||||
A.6 Table C: \(\chi^2\) critical values
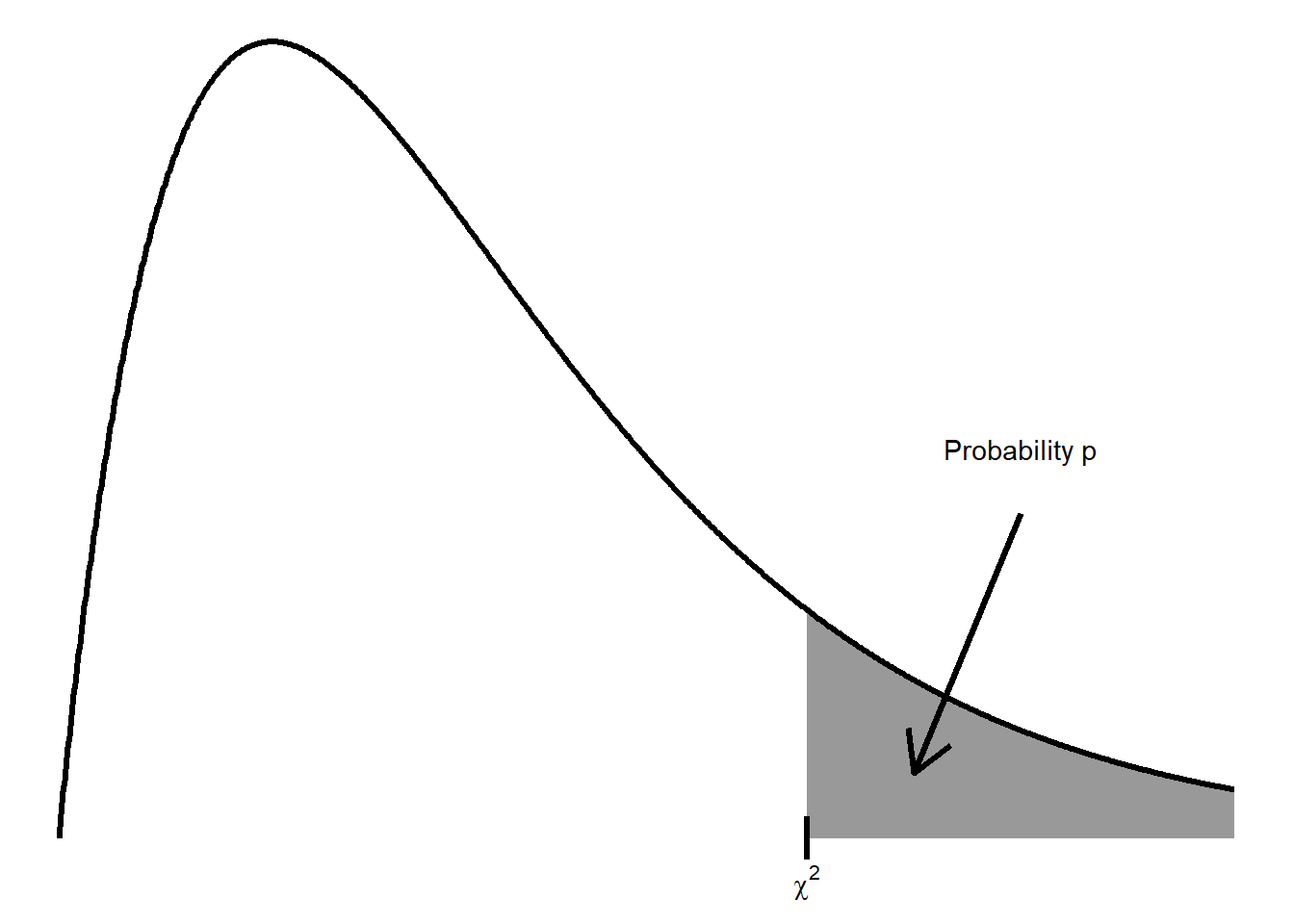
Click here for table of \(\chi^2\) distribution critical values
Table entry for \(p\) is the point (\(\chi^2\)) with probability \(p\) lying above it.
| df | Tail Probability \(p\) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.25 | 0.20 | 0.15 | 0.10 | 0.05 | 0.025 | 0.02 | 0.01 | 0.005 | 0.0025 | 0.001 | 0.0005 | |
| 1 | 1.32 | 1.64 | 2.07 | 2.71 | 3.84 | 5.02 | 5.41 | 6.63 | 7.88 | 9.14 | 10.83 | 12.12 |
| 2 | 2.77 | 3.22 | 3.79 | 4.61 | 5.99 | 7.38 | 7.82 | 9.21 | 10.60 | 11.98 | 13.82 | 15.20 |
| 3 | 4.11 | 4.64 | 5.32 | 6.25 | 7.81 | 9.35 | 9.84 | 11.34 | 12.84 | 14.32 | 16.27 | 17.73 |
| 4 | 5.39 | 5.99 | 6.74 | 7.78 | 9.49 | 11.14 | 11.67 | 13.28 | 14.86 | 16.42 | 18.47 | 20.00 |
| 5 | 6.63 | 7.29 | 8.12 | 9.24 | 11.07 | 12.83 | 13.39 | 15.09 | 16.75 | 18.39 | 20.52 | 22.11 |
| 6 | 7.84 | 8.56 | 9.45 | 10.64 | 12.59 | 14.45 | 15.03 | 16.81 | 18.55 | 20.25 | 22.46 | 24.10 |
| 7 | 9.04 | 9.80 | 10.75 | 12.02 | 14.07 | 16.01 | 16.62 | 18.48 | 20.28 | 22.04 | 24.32 | 26.02 |
| 8 | 10.22 | 11.03 | 12.03 | 13.36 | 15.51 | 17.53 | 18.17 | 20.09 | 21.95 | 23.77 | 26.12 | 27.87 |
| 9 | 11.39 | 12.24 | 13.29 | 14.68 | 16.92 | 19.02 | 19.68 | 21.67 | 23.59 | 25.46 | 27.88 | 29.67 |
| 10 | 12.55 | 13.44 | 14.53 | 15.99 | 18.31 | 20.48 | 21.16 | 23.21 | 25.19 | 27.11 | 29.59 | 31.42 |
| 11 | 13.70 | 14.63 | 15.77 | 17.28 | 19.68 | 21.92 | 22.62 | 24.72 | 26.76 | 28.73 | 31.26 | 33.14 |
| 12 | 14.85 | 15.81 | 16.99 | 18.55 | 21.03 | 23.34 | 24.05 | 26.22 | 28.30 | 30.32 | 32.91 | 34.82 |
| 13 | 15.98 | 16.98 | 18.20 | 19.81 | 22.36 | 24.74 | 25.47 | 27.69 | 29.82 | 31.88 | 34.53 | 36.48 |
| 14 | 17.12 | 18.15 | 19.41 | 21.06 | 23.68 | 26.12 | 26.87 | 29.14 | 31.32 | 33.43 | 36.12 | 38.11 |
| 15 | 18.25 | 19.31 | 20.60 | 22.31 | 25.00 | 27.49 | 28.26 | 30.58 | 32.80 | 34.95 | 37.70 | 39.72 |
| 16 | 19.37 | 20.47 | 21.79 | 23.54 | 26.30 | 28.85 | 29.63 | 32.00 | 34.27 | 36.46 | 39.25 | 41.31 |
| 17 | 20.49 | 21.61 | 22.98 | 24.77 | 27.59 | 30.19 | 31.00 | 33.41 | 35.72 | 37.95 | 40.79 | 42.88 |
| 18 | 21.60 | 22.76 | 24.16 | 25.99 | 28.87 | 31.53 | 32.35 | 34.81 | 37.16 | 39.42 | 42.31 | 44.43 |
| 19 | 22.72 | 23.90 | 25.33 | 27.20 | 30.14 | 32.85 | 33.69 | 36.19 | 38.58 | 40.88 | 43.82 | 45.97 |
| 20 | 23.83 | 25.04 | 26.50 | 28.41 | 31.41 | 34.17 | 35.02 | 37.57 | 40.00 | 42.34 | 45.31 | 47.50 |
| 21 | 24.93 | 26.17 | 27.66 | 29.62 | 32.67 | 35.48 | 36.34 | 38.93 | 41.40 | 43.78 | 46.80 | 49.01 |
| 22 | 26.04 | 27.30 | 28.82 | 30.81 | 33.92 | 36.78 | 37.66 | 40.29 | 42.80 | 45.20 | 48.27 | 50.51 |
| 23 | 27.14 | 28.43 | 29.98 | 32.01 | 35.17 | 38.08 | 38.97 | 41.64 | 44.18 | 46.62 | 49.73 | 52.00 |
| 24 | 28.24 | 29.55 | 31.13 | 33.20 | 36.42 | 39.36 | 40.27 | 42.98 | 45.56 | 48.03 | 51.18 | 53.48 |
| 25 | 29.34 | 30.68 | 32.28 | 34.38 | 37.65 | 40.65 | 41.57 | 44.31 | 46.93 | 49.44 | 52.62 | 54.95 |
| 26 | 30.43 | 31.79 | 33.43 | 35.56 | 38.89 | 41.92 | 42.86 | 45.64 | 48.29 | 50.83 | 54.05 | 56.41 |
| 27 | 31.53 | 32.91 | 34.57 | 36.74 | 40.11 | 43.19 | 44.14 | 46.96 | 49.64 | 52.22 | 55.48 | 57.86 |
| 28 | 32.62 | 34.03 | 35.71 | 37.92 | 41.34 | 44.46 | 45.42 | 48.28 | 50.99 | 53.59 | 56.89 | 59.30 |
| 29 | 33.71 | 35.14 | 36.85 | 39.09 | 42.56 | 45.72 | 46.69 | 49.59 | 52.34 | 54.97 | 58.30 | 60.73 |
| 30 | 34.80 | 36.25 | 37.99 | 40.26 | 43.77 | 46.98 | 47.96 | 50.89 | 53.67 | 56.33 | 59.70 | 62.16 |
| 40 | 45.62 | 47.27 | 49.24 | 51.81 | 55.76 | 59.34 | 60.44 | 63.69 | 66.77 | 69.70 | 73.40 | 76.09 |
| 50 | 56.33 | 58.16 | 60.35 | 63.17 | 67.50 | 71.42 | 72.61 | 76.15 | 79.49 | 82.66 | 86.66 | 89.56 |
| 60 | 66.98 | 68.97 | 71.34 | 74.40 | 79.08 | 83.30 | 84.58 | 88.38 | 91.95 | 95.34 | 99.61 | 102.69 |
| 80 | 88.13 | 90.41 | 93.11 | 96.58 | 101.9 | 106.6 | 108.1 | 112.3 | 116.3 | 120.1 | 124.8 | 128.3 |
| 100 | 109.1 | 111.7 | 114.7 | 118.5 | 124.3 | 129.6 | 131.1 | 135.8 | 140.2 | 144.3 | 149.4 | 153.2 |